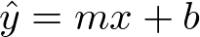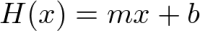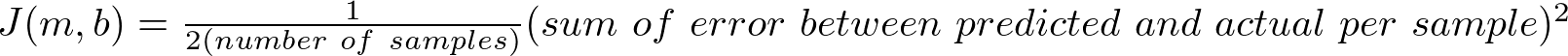Learn forecasting here! We'll go through some basic concepts.

• Predict a y value for every x. y-hat is the predicted value.
• Simple linear model with slope and intercept.

• Linear regression is a model creation procedure:
  • Use J, the cost function, to measure which models are better (with less error):

• J is arbitrary, but the one listed above is a rough overview of least-squares error. It is also referred to as Sum of Squared Error (SSE).

• There are different ways of optimizing H(x) using J, including gradient descent, which involves using the gradient of J to find a point where all parts of the gradient are 0.
• When the gradient is 0, the function given has the least amount of error.
  • Catch: just because gradient = 0 doesn't mean that it's a global minimum!
• We can solve for the zero-point of the gradient using calculus and the partial derivative of J with respect to x or each of x1, x2, x3, etc.. if there is more than one feature you use to find y.

• Use the cost function, J, to optimize, H, the prediction model.
• Here, H is a linear function: H(x) = mx + b.
• J is often SSE/least square error.
• Apply linear algebra when the data grows to a larger amount of input features: Y = AX + B.

• Split a group of data into K groups of equal size.
• Use a certain amount of groups as the training, then use the rest as test data.
• Use all combinations of training/test data across the folds to get multiple models.
• Aggregate the models somehow to get a final model.

• Split the data between training and test, get models, aggregate models.

Coming soon…

Coming soon…

Coming soon…

We should cover SLINK and CLINK, algorithms that turn it from a regular O(n^3) or even O(2^n) to O(n^2) time complexity.

This has been called an award-winning clustering method based on a density. From Wikipedia.

A better alternative to DBSCAN so it says on Wikipedia.

Coming soon…

Coming soon…

Coming soon…

Coming soon…

Coming soon…

Euclidean, Manhattan, Mahalanobis distance. Perhaps briefly mention string-distance algorithms (for text and stuff).

IMPORTANT!!!

Coming soon…

Coming soon…

Coming soon…

e.g. DeLorean, Monocle as applied to these dataset–take a reduced dimensionality graph minimum spanning tree, plot the longest path through it, this path represents a nice progression that can be thought of a varying along a “pseudotime” variable related to the change in expression of features as it goes along.

Probably not worth looking at.

Weather prediction seems to be needed to be solved by some application of Bayesian statistics–it's a bit shallow to assume that the features that we possess are all that affects the weather–however, it is also bad to challenge Occam's Razor, the principle that simpler models are better. Other scientists have utilized this heuristic in order to produce good theories (quantum mechanics, relativity, etc.). However, the weather is clearly not so easy to solve (weather forecasts can still be off sometimes, right?) and through some preliminary research, it may have to do with chaos theory.

Chaos theory deals with systems that are probably not linear, and behave more like the cryptography hashes–small changes in the initial/input state result in greatly different behaviors. Apparently the weather works like this too. But, what if the problem is that there are, in fact, many different factors that include the final, observed features in a non-linear fashion? Perhaps the final solution isn't going to be linear, but still perhaps predictable with the correct linear model.

It's clear that linear models will not work for weather prediction, especially in the event of an unusual event, such as a storm, hurricane, or even a tsunami. So our endgame is going to end up here, I'm guessing.

Contributing authors:

Created by atasato on 2016/02/02 09:17.